AVL树（微观版）

· 2021-02-20 · # 数据结构

AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。 --摘自百度百科
显然G. M. Adelson-Velsky贡献更大，是距今已有59年的老技术遗产。让人联想起同样拥有60多年历史的神经网络老模型理论，得益于现代硬件技术的提升，总算能够真正发挥实力，结果一鸣惊人，飞速发展。
小学生必知必会

序言

前置知识点：二叉排序树 Binary Sort Tree
在二叉排序树BST结构中已讨论过，BST从根本上提供了一种将杂乱数据进行有序组织的方式，从而帮助我们高效快速的检索和排名。但它最大的缺陷是非常依赖输入数据的分布和操作顺序，一旦遇到了一个非常有序的数据集，BST就会退化成了普通链表，失去性能优势（原因是BST的根节点永远不会变化）。因此科学家提出了「可自适应调整的平衡二叉排序树」, 简称 "平衡二叉排序树"。无论我们怎样操作数据进行插入或删除，最终的树形结构始终都能保持平衡，不会退化成一条链表。
自然而然地，我们能够想到这样的数据结构在我们进行插入或删除数据时，它一定是内部存在着某种自适应的调整（动态改变根节点），维持着整体树的平衡，因此这些调整也是隐形的开销。

平衡二叉树关键词：平衡、调整。
思考：

如何定义一棵树是否平衡？ 「平衡条件」

根据平衡定义，如何进行自适应调整？ 「调整方式」

平衡二叉排序树是一个大类，里面可以细分出太多种不同的模型，任何一种平衡二叉排序树模型都必须要准确回答上面两个问题。
细分的平衡BST模型之间的不同可以简单归纳为平衡条件的不同，从而产生不同的调整方式。

性质

AVL树是平衡二叉排序树中的一种，且目前而言应该是其中最完美平衡的一个，因为它的平衡条件特别苛刻, 反过来说它的平衡条件也非常合乎常理。
非常直观地，我们若想要一棵二叉树尽可能的平衡，就是希望每一个节点的左子树和右子树高度尽可能都相等, 让整棵树的高度尽可能的矮一些。那么如何将这种思想按某种规则量化呢？很简单即左子树和右子树的高度差不能大于1：

|H(left) - H(right)| <= 1

这也是AVL树定义的平衡条件规则。因此只要基于这条规则，AVL树就不可能退化成一条链表结构。

注意：

平衡二叉排序树的本质依然是二叉排序树，所以拥有二叉排序树的所有性质
平衡二叉排序树的学习重点在于：「平衡条件」及「平衡调整方式」的学习。

提一句：只要喜欢也可以自由更改平衡条件，使左右子树的高度差不大于2或3等等。可以思考哪种平衡条件更严苛？平衡条件的宽松和严苛有什么好处和坏处？
还有一种目前工程应用最广泛的平衡二叉排序树结构「红黑树」，平衡条件相对宽松，但平衡条件比较抽象，第一次很难直观理解。

思考

思考1. 高度为H的BST (二叉排序树)，所包含节点的数量在什么范围（最多和最少）？

$H \le size \le 2^H - 1$

思考2. 高度为H的AVL树，所包含节点的数量在什么范围（最多和最少）？

假设 low(h) 代表高度为h 的AVL树最少包含的节点数目。
然后我们在左右子树分别放高度为 H-1的树和 H-2的树，引出下式：
$low(H-2) + low(H-1) + 1 \le size \le 2^H - 1$ $l o w (H - 2) + l o w (H - 1) + 1 \leq s i z e \leq 2^{H} - 1$
- 斐波那契数列的增长速度大概是 $1.618^n$
- $1.618^H \le size \le 2^H - 1$

结论：节点数量N 与树高H 的关系大概是 H = log(N)

思考3. 根据AVL树的平衡条件，你能尽可能的在纸上罗列出多少种不平衡的样例？能否看到一点点规律出来？

数据的插入和删除

因为本质上就是BST，所以这部分与BST的操作一模一样。
关键在于插入或删除操作后有可能破坏AVL树制定的平衡条件规则，因此最后只需要多增加平衡调整操作。

调整条件（4种失横类型）

答思考3：根据前辈们的研究，一共总结归纳出4种失衡类型：LL, LR, RL, RR。
一般操作是站在父节点root看俩子节点高度差是否大于1，若失衡（大于1），则再向下一层查看孙子节点，找出是属于哪一种失衡类型？

特别需要注意一点：
要明白我们说root节点失衡了，需要调整，表示：只在root节点向下看时是失衡状态，但是root节点的内部(左右分支)任意节点向下看全都是平衡的。这点非常重要，关系到调整策略的生效。（比如我们从最初的根节点就发现失衡，向下看一看左右分支也失衡，那么不能立刻调整根节点，需要向下找到最一线的失衡节点，然后再向上回溯调整。）因为我们的调整策略是失衡节点调整后不会影响节点下面的平衡性，而有可能影响节点上面的平衡性。

思考4：树形结构的失衡调整大致都是两种操作：左旋+右旋。能试试自己旋转调整4种失衡类型吗？

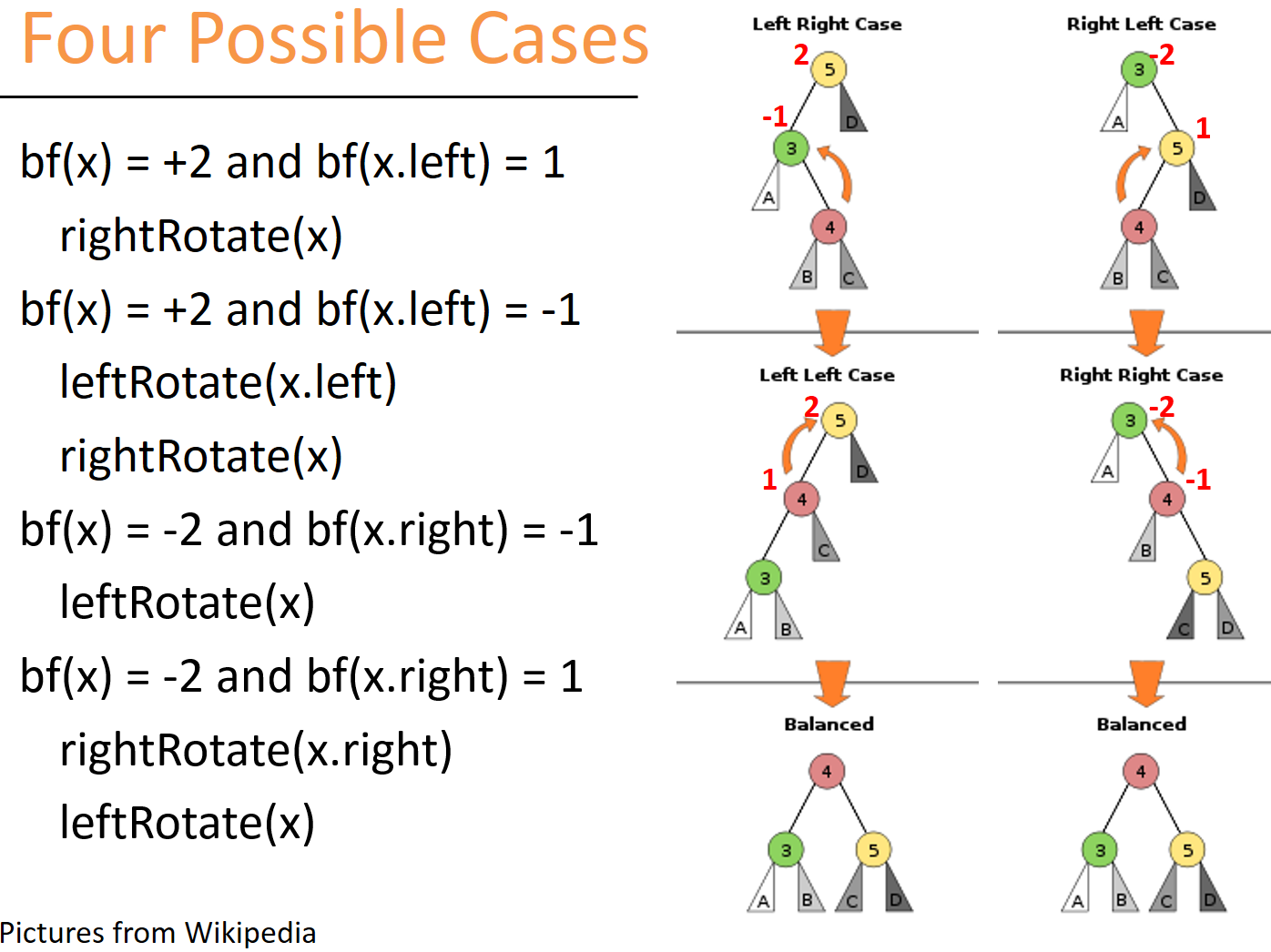
调整策略

LL型和 RR型
- LL型：直接拿root大右旋。（上图+2 +1型）
- RR型：直接拿root大左旋。（上图-2 -1型）
LR型和 RL型
- LR：先拿root的左子树小左旋变成 LL，再拿root大右旋平衡。（上图+2 -1型）
- RL：先拿root的右子树小右旋变成 RR，再拿root大左旋平衡。（上图-2 +1型）

平衡调整策略：

发生在回溯阶段时，出现的第一个失衡节点处。
理解平衡调整策略的关键在于：分析清楚四种情况下，ABCD四棵子树树高的关系
LR 和 LL 可以写在一起；RL 和 RR 可以写在一起。

思考5：LL类型能否直接用小右旋代替？在什么情况下不能？
思考6：旋转前后，哪些节点的高度是不变的？哪些节点的高度是会变的？
思考7：为什么说AVL插入新节点所需要的最大旋转次数是常数，不需要一直旋转到根节点？为什么AVL删除节点后的调整有可能会旋转到根节点？

关键代码演示

1. NIL节点

Node __NIL;
#define NIL (&__NIL)
__attribute__((constructor))
void init_NIL(){
    NIL->key = NIL->h = 0;
    NIL->lchild = NIL->rchild = NIL;
    return ;
}

NIL节点是一种特殊的节点，它的左右子节点都指向自己。
在AVL树的实现中，我们用制造的NIL节点来代替NULL，这是一种编码技巧。
代码解释：
__attribute__((constructor)) 表示令接下来的函数在main()函数之前就执行。（当然不附加这条属性，在main()函数内部的第一行执行init_NIL()函数是一样的效果）

2. 调整策略代码

Node *maintain(Node *root) {
    if (abs(H(L(root)) - H(R(root))) <= 1) return root;
    if (H(L(root)) > H(R(root))) {
        // L 型：LL or LR
        if (H(L(L(root))) < H(R(L(root)))) {
            // 这种多层结构时 NIL 的作用就发挥出来了，否则要加很多判断
            root->lchild = left_rotate(root->lchild); // LR 小左旋；
        }
        root = right_rotate(root); // 最后一定要大右旋；
    } else {
        // R 型：RR or RL
        if (H(R(R(root))) < H(L(R(root)))) {
            // 右子树的 左侧更高
            root->rchild = right_rotate(root->rchild); //RL 小右旋
        }
        root = left_rotate(root); // 一样无论RR 或 RL 最后都要大左旋
    }
    return root;
}

思考7：maintain()调整能否只用在插入或删除位置一次，而不在整个回溯过程每个位置都做调整？即当前节点调整平衡了，父节点是不是也就平衡了？什么情况下不是？

3. 左旋和右旋代码

Node *left_rotate(Node *root) {
    Node *p = root->rchild;
    root->rchild = p->lchild;
    p->lchild = root;
    update_height(root);
    update_height(p);
    return p;
}

Node *right_rotate(Node *root) {
    Node *p = root->lchild;
    root->lchild = p->rchild;
    p->rchild = root;
    update_height(root);
    update_height(p);
    return p;
}

尤其注意一个易错点：左旋和右旋后，要更新两个节点的height，两点高度有变化。
而且必须是先更新root 再更新p。因为旋转完成后，root 实际到了 p 的下面。

思考8：既然maintain()里包括rotate操作，rotate操作里也都有update_height()。是不是我们不需要在回溯过程中再更新update_height？不是。

完整代码

最基础的AVL树实现：

#include <stdio.h>
#include <stdlib.h>
#define H(a) (a->h)
#define L(a) (a->lchild)
#define R(a) (a->rchild)

typedef struct Node {
    int key, h;
    struct Node *lchild, *rchild;
} Node;

Node __NIL;
#define NIL (&__NIL)
__attribute__((constructor))
void init_NIL() {
    NIL->key = NIL->h = 0;
    NIL->lchild = NIL->rchild = NIL;
    return ;
}

Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->h = 1;
    p->lchild = p->rchild = NIL;
    return p;
}

void update_height(Node *root) {
    root->h = (H(L(root)) > H(R(root)) ? H(L(root)) : H(R(root))) + 1;
    return ;
}

Node *left_rotate(Node *root) {
    Node *p = root->rchild;
    root->rchild = p->lchild;
    p->lchild = root;
    update_height(root);
    update_height(p);
    return p;
}

Node *right_rotate(Node *root) {
    Node *p = root->lchild;
    root->lchild = p->rchild;
    p->rchild = root;
    update_height(root);
    update_height(p);
    return p;
}

Node *maintain(Node *root) {
    if (abs(H(L(root)) - H(R(root))) <= 1) return root;
    if (H(L(root)) > H(R(root))) {
        // LL LR
        if (H(R(L(root))) > H(L(L(root)))) {
            root->lchild = left_rotate(root->lchild);
        }
        root = right_rotate(root);
    } else {
        // RR RL
        if (H(L(R(root))) > H(R(R(root)))) {
            root->rchild = right_rotate(root->rchild);
        }
        root = left_rotate(root);
    }
    return root;
}

Node *insert(Node *root, int key) {
    if (root == NIL) return getNewNode(key);
    if (root->key == key) return root;
    else if (root->key > key) root->lchild = insert(root->lchild, key);
    else root->rchild = insert(root->rchild, key);
    update_height(root);
    return maintain(root);
}

Node *predecessor(Node *root) {
    Node *p = root->lchild;
    while (p->rchild != NIL) p = p->rchild;
    return p;
}

Node *erase(Node *root, int key) {
    if (root == NIL) return NIL;
    if (root->key > key) {
        root->lchild = erase(root->lchild, key);
    } else if (root->key < key) {
        root->rchild = erase(root->rchild, key);
    } else {
        if (root->lchild == NIL || root->rchild == NIL) {
            Node *p = root->lchild == NIL ? root->rchild : root->lchild;
            free(root);
            return p;
        } else {
            Node *p = predecessor(root);
            root->key = p->key;
            root->lchild = erase(root->lchild, p->key);
        }
    }
    update_height(root);
    return maintain(root);
}

void clear(Node *root) {
    if (root == NIL) return;
    clear(root->lchild);
    clear(root->rchild);
    free(root);
    return ;
}

void printNode(Node *root) {
    printf("(%d [%d], %d, %d)\n",
          root->key, root->h,
          root->lchild->key,
          root->rchild->key);
}

void output(Node *root) {
    if (root == NIL) return;
    output(root->lchild);
    printNode(root);
    output(root->rchild);
    return ;
}

int main() {
    //init_NIL();
    int op, val;
    Node *root = NIL;
    while(~scanf("%d%d", &op, &val)) {
        getchar();
        switch(op) {
            case 0: root = erase(root, val); break;
            case 1: root = insert(root, val); break;
        }
        output(root);
        printf("----------------\n");
    }
    return 0;
}

课外思考

问题：普通BS树一定比高级AVL树差吗？

答：当然不一定！BS树的性能很大程度上是根据插入数据的顺序决定的。可以看出AVL树是改进普通BS树的性能下限，而不是提高上限。即使用AVL树，不管数据多么乱，性能再差也不会差多少，因此实际工程中通常青睐AVL树。但并非意味着BS树不好，只用BS树的话性能需要由输入数据决定，拼运气。
对BS树来说，最好的数据输入情况是直接形成一个完全二叉树；最坏的情况是一个完全有序的数据，退化成一个链表。AVL树的话，经过调整，一般总是完全二叉树。
上升一下人生观，有的人不学习但依然生活得很好，很大程度是运气好，类似BST。但是学习和提升成绩至少能提升我们的下限，避免到太糟糕的情况。

小结：

AVL树改进的是节点数量的下限
树高 = 生命长度，节点数量 = 生命财富，不同的算法达到的结果也不一样
教育提升的是下限，而非上限。上限取决于能力和运气。

AVL树的兄弟 -- SB树

与AVL树几乎一致，AVL树用节点的高度来作为平衡依据，而SB树用节点的大小size作为平衡依据。

|Size(left) - Size(right)| <= 1

总结

代码部分：

插入和删除以后，注意重新计算树高字段。
插入和删除操作，每一次回溯return的都是已调整好的节点。
平衡调整判断四种失衡形态，进行相应左旋和右旋，左旋右旋结束后也要重新计算树高字段。
引入了NIL字段，用来代替NULL（注意所有的NULL都要用NIL代替），NULL不可以访问字段，但是NIL是一个实际节点，可访问。（NIL字段在红黑树里是非常重要的，否则代码变得极其复杂）

模型部分：
AVL树极适合作为平衡二叉排序树学习的入门结构。它的平衡条件和策略都非常地直观和容易理解，因此代码也不复杂。
AVL树的平衡条件非常严苛，所以AVL树常常都是完美二叉树的状态，使数据检索和排名的性能能达到最优。
但是在代码模拟中就可以发现，这种严苛的平衡条件，代价是频繁的树结构调整，无论数据插入或删除。
在工程应用中，经常要考虑数据量极大的情况，例如几秒钟百万次操作的情况？此时用频繁调整的巨大开销来换取最极速检索效率是否值得呢？

练习题目：
1066 Root of AVL Tree

目前在工程中应用最为广泛的平衡二叉排序结构是「红黑树」，它实际上牺牲了极小一部分检索效率性能，换来降低频繁平衡调整的可能性，总体而言开销更小。下一章学习初中生必知必会：红黑树。