When improving the model parameters of machine learning algorithms, that is, unconstrained optimalization problem.
Gradient Descent method is one of most common used methods. The other one is the least square method. Here is a complete summary of the gradient descent method.

1. What is gradient?

In calculus, Gradient is to find the partial derivatives of the parameters of the multivariate function, and write all partial derivative of the obtained parameters in the form of one vector. For the function f(x, y) as an example, finding the partial derivatives of x and y, then the gradient vector is $ (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y})^T $, AKA grad f(x, y) or $ \nabla f(x,y)$

The specific gradient vector value at point (x0, y0) is $ (\frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial y_0})^T $ or $ \nabla f(x_0,y_0)$

If there are three parameters, then gradient vector is $ (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z})^T $, and so on.

In geometrically speaking, the meaning of gradient is the direction where the function f(x,y) changes fastest. At point (x0, y0), the direction of gradient vector $(\frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial y_0})^T $ is where f(x,y) changes fastest.

If we keep following the gradient vector direction, we will reach the maximum or minimum point of function faster and easier.

2. Gradient Descent

Assume we are somewhere on a large mountain, because we don’t know how to go down the mountain, so we decided to take one step at a time. That is, we can take a step down from the current position's steepest direction, and then continue to calculate the gradient of the new position and take a step toward the position where the step is located at the steepest and easiest to descend. Going on like this step by step until we feel that we have reached the foot of the mountain.
gd

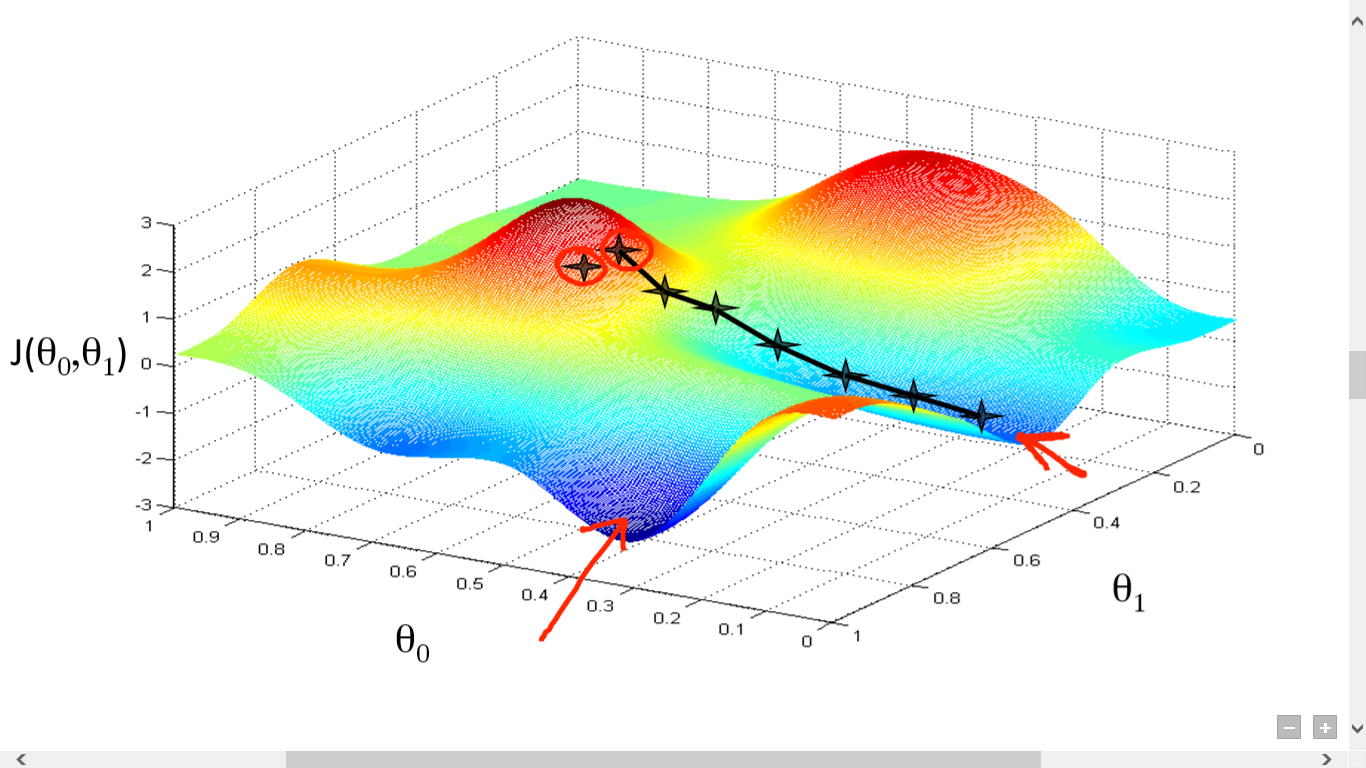
Of course, if we go on like this, we may not be able to reach the foot of the mountain, but to a certain foot in a local part of the mountain.

As can be seen from the above explanation, gradient descent may not necessarily find the global optimal solution, but may be a local optimal solution. Of course, if the loss function is convex, the solution obtained by the gradient descent method must be the global optimal solution.

3. Concepts of gradient descent

  • Learining Rate: The step size determines the length of each step in the negative direction of the gradient during the gradient descent iteration.
  • Feature: Refers to the input part of the sample data. (x0(1),x1(1),...,xn(1),y1)(x_0^{(1)},x_1^{(1)},...,x_n^{(1)},y_1)
  • Hypothesis Function: In supervised learning, the hypothesis function used to fit the input samples, denoted as hθ(X)h_\theta(X). For example, the linear regression hypothesis model is hθ(x1,x2,...,xn)=θ0+θ1x1+θ2x2+...+θnxnh_\theta(x_1,x_2,...,x_n) = \theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n
  • Loss Function: In order to evaluate how well the model fits the data, a loss function is usually used to measure the degree of fit. The minimization of the loss function means that the degree of fitting is the best and the corresponding model parameters are the optimal parameters. In linear regression model, the loss function usually squares the difference between the sample output (yi) and the hypothesis function output (y hat).

If there is a linear regression model for m samples: (x1i,x2i,...,xni,yi),i=(1,2,...,m)(x_1^{i},x_2^{i},...,x_n^{i},y_i),i=(1,2,...,m), the loss function is:

J(θ0,θ1,...,θn)=∑i=1m(hθ(x1(i),x2(i),...,xn(i))−yi)2J(\theta_0,\theta_1,...,\theta_n) = \sum_{i=1}^m(h_\theta(x_1^{(i)},x_2^{(i)},...,x_n^{(i)})-y_i)^2

x(i)x^{(i)} is the feature of the i-th sample data.
yiy_i is the output of the i-th sample data.
hθ(x1(i),x2(i),...,xn(i))h_\theta(x_1^{(i)},x_2^{(i)},...,x_n^{(i)}) is the Hypothesis Function. (== y^\widehat{y})

4. Gradient Descent Algorithm

The algorithm of gradient descent method can have two expressions: algebraic method and matrix method (also called vector method).

4.1 Algebraic Expression

1. Prerequite: Set Hypothesis Function and Loss Function of the optimization model. Assume Hypothesis Function is the linear regression model. Then the loss function is:

J(θ0,θ1,...,θn)=12m∑i=1m(hθ(x1(i),x2(i),...,xn(i))−yi)2J(\theta_0,\theta_1,...,\theta_n) = \frac{1}{2m}\sum_{i=1}^m(h_\theta(x_1^{(i)},x_2^{(i)},...,x_n^{(i)})-y_i)^2

1/2m is a new factor we added. 1/m means average. 1/2 is mainly to facilitate the calculation of later partial derivatives. We know that m is a constant greater than zero, so it has no effect on the nature of the function gradient. It does not change the θ\theta when we get the minimum value of J(θ)J(\theta). After all, what we need is only the θ\theta, not the minimum value of J(θ)J(\theta).

2. Initialize some algorithm parameters:

  • Initialize all (θ0,θ1,...,θn)(\theta_0,\theta_1,...,\theta_n).
  • Learning Rate α\alpha. (Step Size)
  • Algorithm termination distance ε\varepsilon. If the distance of gradient descent is less than ε\varepsilon, algorithm stoppes.

For example, in the absence of any prior knowledge, we can simply intialize all θ\theta to 0 and α\alpha to 1. Then Optimize them again when tuning is needed.

3. Algorithm Process:

  • Step 1: Calculate the gradient of current position. For θj\theta_j, its gradient expression is:

    ∂∂θjJ(θ0,θ1,...,θn)\frac{\partial}{\partial\theta_j} J(\theta_0,\theta_1,...,\theta_n)

j is (0,1,2,...,n), represents the j-th parameter.

  • Step 2: Multiply Gradient by Learning Rate α\alpha (step size) to get the distance of gradient descent at current position. That is, α∂∂θjJ(θ0,θ1,...,θn)\alpha\frac{\partial}{\partial\theta_j} J(\theta_0,\theta_1,...,\theta_n)

  • Step 3: If all θj\theta_j's distance of gradient descent is less than ε\varepsilon, algorithm stopped. And current (θ0,θ1,...,θn)(\theta_0,\theta_1,...,\theta_n) is returned as the final result.

  • Step 4: Update all θj\theta_j and jump to Step 1 for a new loop. The update expression is as follows:

    θj=θj−α∂∂θjJ(θ0,θ1,...,θn)\theta_j = \theta_j - \alpha\frac{\partial}{\partial\theta_j} J(\theta_0,\theta_1,...,\theta_n)

The algorithm is very simple and elegant, the key point is how to calculate ∂∂θjJ(θ0,θ1,...,θn)\frac{\partial}{\partial\theta_j} J(\theta_0,\theta_1,...,\theta_n):

J(θ0,θ1,...,θn)=12m∑i=1m(hθ(x1(i),x2(i),...,xn(i))−yi)2J(\theta_0,\theta_1,...,\theta_n) = \frac{1}{2m}\sum_{i=1}^m(h_\theta(x_1^{(i)},x_2^{(i)},...,x_n^{(i)})-y_i)^2

∂∂θjJ(θ0,θ1,...,θn)=1m∑i=1m(hθ(x1(i),x2(i),...,xn(i))−yi)xj(i)\frac{\partial}{\partial\theta_j} J(\theta_0,\theta_1,...,\theta_n) = \frac{1}{m}\sum_{i=1}^m(h_\theta(x_1^{(i)},x_2^{(i)},...,x_n^{(i)})-y_i)x_j^{(i)}

θj=θj−α∑i=1m(hθ(x1(i),x2(i),...,xn(i))−yi)xj(i)\theta_j = \theta_j - \alpha\sum_{i=1}^m(h_\theta(x_1^{(i)},x_2^{(i)},...,x_n^{(i)})-y_i)x_j^{(i)}

4.2 Matrix Expression

Algebraic Expression and Matrix Expression are essentially the same, but the representation of Matrix will be more concise. Suppose we have m sample data: (x1(1),x2(1),...,xn(1),y1),(x1(2),x2(2),...,xn(2),y2),...,(x1(m),x2(m),...,xn(m),ym)(x_1^{(1)},x_2^{(1)},...,x_n^{(1)},y_1),(x_1^{(2)},x_2^{(2)},...,x_n^{(2)},y_2),...,(x_1^{(m)},x_2^{(m)},...,x_n^{(m)},y_m)

1. Prerequite: Set Hypothesis Function and Loss Function of the optimization model. Assume Hypothesis Function is the linear regression model:

hθ(X)=Xθh_\theta(X) = X\theta

J(θ)=12(Xθ−Y)T(Xθ−Y)J(\theta) = \frac{1}{2}(X\theta-Y)^T(X\theta-Y)

X is a m×nm \times n matrix (m records and n features).
θ\theta is a n×1n \times 1 vector (n coefficients of n features).
hθ(X)h_\theta(X) is a m×1m\times 1 vector (m prediction y value of m sample records)
Y is a m×1m\times 1 vector (m actual y value of m sample records)

2. Initialize some algorithm parameters: Same as 4.1 section.
3. Algorithm Process: Same as 4.1 section.

∂∂θJ(θ)=XT(Xθ−Y)\frac{\partial}{\partial\theta}J(\theta) = X^T(X\theta-Y)

θ=θ−α∂∂θJ(θ)=θ−αXT(Xθ−Y)\begin{aligned} \theta &= \theta - \alpha\frac{\partial}{\partial\theta}J(\theta)\\ &= \theta - \alpha X^T(X\theta-Y) \end{aligned}

Matrix derivative chain rule:
Formula 1: ∂∂X(XTX)=2X\frac{\partial}{\partial X}(X^TX) = 2X
Formula 2: $ \nabla_xf(AX+B) = A^T $

5. Tuning of gradient descent algorithm

  • Learning Rate: If the step size is too large, the iteration will be too fast, and it may even miss the optimal solution. The step size is too small, the iteration speed is too slow, and the algorithm cannot end for a long time. So the step size of the algorithm needs to be run multiple times to get a better value.
  • θ\theta initialization: different intial parameter value may lead to different minimum value. Hence, the gradient descent only finds the local minimum. if the loss function is a convex function, it must be the global optimal solution. It is necessary to run the algorithm with different initial values multiple times, which can increase the possibility that we skip the local minimum to reach the global minimum.
  • Normalized: The data range of different features is different, if some features' data value are very high, and some others' are very low, it may lead to a very slow iteration. In order to reduce the influence of the feature value, the feature data can be normalized. For each xj feature's data, we transform it to:

    xj=xj−xj‾std(xj)x_j = \frac{x_j - \overline{x_j}}{std(x_j)}

xjx_j becomes a new feature with new expectation 0 and new variance 1, the iteration speed can be greatly accelerated.

6. Gradient Descent Family (BGD, SGD, MBGD)

6.1 BGD (Batch Gradient Descent)

Batch Gradient Descent is the most commonly used form. It always uses all m sample data when we update parameter θ\theta once. As discuss above:

θj=θj−α∑i=1m(hθ(x1(i),x2(i),...,xn(i))−yi)xj(i)\theta_j = \theta_j - \alpha\sum_{i=1}^m(h_\theta(x_1^{(i)},x_2^{(i)},...,x_n^{(i)})-y_i)x_j^{(i)}

For each iteration of one of θ\theta, we use all m samples to caculate gradient.

6.2 SGD (Stochastic Gradient Descent)

Stochastic Gradient Descent is similar to the BGD, the difference is that SGD use only one random sample to calculate gradient:

θj=θj−α(hθ(x1(i),x2(i),...,xn(i))−yi)xj(i)\theta_j = \theta_j - \alpha(h_\theta(x_1^{(i)},x_2^{(i)},...,x_n^{(i)})-y_i)x_j^{(i)}

BGD and SGD are two extremes. One uses all data for gradient descent, and one uses only one sample data for gradient descent. Advantages and disadvantages are very prominent.

  1. Traning Speed: SGD is very fast, since it uses only one sample to iterate each time. While the BGD cannot satisfy the training speed when the sample size is large.
  2. Accuracy: SGD uses only one sample, most likely resulting in a not optimal solution.
  3. convergence Speed: SGD uses one sample at a interation, the iteration direction changes greatly, and it cannot quickly converge to the local optimal solution.

Is there a moderate method to neutralize the advantages and disadvantages of BGD and SGD? Yes, MBGD

6.3 MBGD (Mini-batch Gradient Descent)

The Mini-batch Gradient Descent is a compromise between the BGD and the SGD, that is, for all m samples, we use k samples to iterate, 0<k<m0<k<m.
Of course, the value of k can be adjusted according to the sample data. The iteration formula is:

θj=θj−α∑i=tt+k−1(hθ(x1(i),x2(i),...,xn(i))−yi)xj(i)\theta_j = \theta_j - \alpha\sum_{i=t}^{t+k-1}(h_\theta(x_1^{(i)},x_2^{(i)},...,x_n^{(i)})-y_i)x_j^{(i)}

7. Comparison of gradient descent method and other optimization algorithms

In machine learning, there are generally these optimization algorithms:

  • Gradient Descent
  • Least Square
  • Newton's method and Quasi-Newton's method

Gradient Descent and Lease Square:

  • Gradient Descent needs step size, Lease Square doesn't.
  • Gradient Descent is an iterative solution, and the Least Square is an analytical solution. If the sample size is not very large, and there is an analytical solution, the Least Square has an advantage over the Gradient Descent, and the LS calculation speed is fast. However, if the sample size is large, Least Square requires a super large inverse matrix, which is difficult or slow to solve the analytical solution. Then iterative Gradient Descent is better.

Gradient Descent and Newton's method/Quasi-Newton's method:

  • Both of them are iterative solution.
  • Gradient Descent is gradient solution. Newton's method is solved by using the inverse or pseudo-inverse matrix of the second-order Hessian matrix.
  • Newton method / Quasi-Newton's method converges faster. But each iteration takes longer than gradient descent

Python implementation Example

  1. f(x)=x2+1f(x)=x^2+1
"""
One Dimensional Gradient Descent Example -- One feature 
"""


def func_1d(x):
    """
    Objective Function
    :param x: independent variable, scalar
    :return: dependent variable, scalar
    """
    return x ** 2 + 1


def grad_1d(x):
    """
    Gradient of Objective Function
    :param x: independent variable, scalar
    :return: dependent variable, scalar
    """
    return x * 2


def gradient_descent_1d(grad, cur_x=0.1, learning_rate=0.01, precision=0.0001, max_iters=10000):
    """
    One-dimensional gradient descent algorithm
    :param grad: Gradient Fuction of Objective Function
    :param cur_x: Current x value
    :param learning_rate: step size
    :param precision: Set convergence accuracy (stop condition)
    :param max_iters: max number of iterations
    :return: local minumum x*
    """
    for i in range(max_iters):
        grad_cur = grad(cur_x)
        if abs(grad_cur) < precision:
        	# when the gradient approaches 0, it is regarded as convergence
            break  
        cur_x = cur_x - grad_cur * learning_rate
        print("The", i, "-th iteration's x value: ", cur_x)

    print("Local Minumum x =", cur_x)
    return cur_x


if __name__ == '__main__':
    gradient_descent_1d(grad_1d, cur_x=10, learning_rate=0.2, precision=0.000001, max_iters=10000)
  1. f(x,y)=−e−(x2+y2)f(x,y) = -e^{-(x^2+y^2)}
"""
2-Dimensional Gradient Descent example -- 2 features
"""
import math
import numpy as np


def func_2d(x):
    """
    Objective Function
    :param x: independent variable, 2d vector
    :return: dependent variable, scalar
    """
    return - math.exp(-(x[0] ** 2 + x[1] ** 2))


def grad_2d(x):
    """
    Gradient of the Objective Function
    :param x: independent variable, 2d vector
    :return: dependent variable, 2d vector
    """
    deriv0 = 2 * x[0] * math.exp(-(x[0] ** 2 + x[1] ** 2))
    deriv1 = 2 * x[1] * math.exp(-(x[0] ** 2 + x[1] ** 2))
    return np.array([deriv0, deriv1])


def gradient_descent_2d(grad, cur_x=np.array([0.1, 0.1]), learning_rate=0.01, precision=0.0001, max_iters=10000):
    """
    2D gradient descent algorithm
    :param grad: Gradient Fuction of Objective Function
    :param cur_x: Current x value (Parameter Initialization)
    :param learning_rate: step size
    :param precision: Set convergence accuracy (stop condition)
    :param max_iters: max number of iterations
    :return: Local minimum x*
    """
    print(f"{cur_x} as the Initialization...")
    for i in range(max_iters):
        grad_cur = grad(cur_x)
        if np.linalg.norm(grad_cur, ord=2) < precision:
        	# when the gradient approaches 0, it is regarded as convergence
            break  
        cur_x = cur_x - grad_cur * learning_rate
        print("The", i, "-th iteration's x value: ", cur_x)

    print("Local minimum x =", cur_x)
    return cur_x


if __name__ == '__main__':
    gradient_descent_2d(grad_2d, cur_x=np.array([1, -1]), learning_rate=0.2, precision=0.000001, max_iters=10000)
  1. f(x1,x2,x3)=3x1+4x2+5x3+6f(x_1,x_2,x_3) = 3x_1+4x_2+5x_3+6
"""
Parameter Estimation
Multiple linear regression gradient descent example (Matrix Method)

Dataset(4 points on the function):
x1, x2, x3, b,  y
1,  1,  2,  1,  23
2,  4,  3,  1,  43
3,  2,  4,  1,  43
4,  3,  1,  1,  35
"""
import numpy as np

def gradient_descent(theta, X, Y, lr=0.01, precision=0.0001, max_iters=10000):
    """
    matrix gradient descent algorithm
    :param theta: parameter estimation of the objective function
    :param X: sample data, independent data, mxn matrix
    :param Y: sample data, dependent data, mx1 matrix
    :param lr: step size
    :param precision: Set convergence accuracy (stop condition)
    :param max_iters: max number of iterations
    :return: Local minimum theta*
    """
    print(f"{theta} as the Initialization...")
    for i in range(max_iters):
        distance = lr*X.T*(X*theta-Y)
        if np.linalg.norm(distance, ord=2) < precision:
            # when the gradient approaches 0, it is regarded as convergence
            print("total iterations:", i)
            break
        theta = theta-distance

    print("Local minimum theta =\n", theta)
    return theta


x = np.mat([[1,1,2,1],[2,4,3,1],[3,2,4,1],[4,3,1,1]])
y = np.mat([[23],[43],[43],[35]])
theta = np.mat([[0],[0],[0],[0]])	
gradient_descent(theta, x, y)

#####
[[0]
 [0]
 [0]
 [0]] as the Initialization...

total iterations: 1852
Local minimum theta =
 [[3.00521152]
 [4.00294095]
 [5.00623515]
 [5.96159285]]

"""
Additional code -- np.linalg.norm

linalg = linear algebra
"""
x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)

import numpy as np
x = np.array([
    [0, 3, 4],
    [1, 6, 4]])

# np.sqrt(0+9+16+1+36+16)
print("Default(sqrt of square sum of all elements, does not return matrix), keepdims=False:\n",np.linalg.norm(x))
print("Sqrt of square sum of all elements, return matrix, keepdims=True:\n",np.linalg.norm(x,keepdims=True))

print("***********************")
# np.sqrt(0+9+16), np.sqrt(1+36+16)
print("Matrix's row vector, l2 norm, axis=1:\n",np.linalg.norm(x,axis=1,keepdims=True))
# np.sqrt(0+1), np.sqrt(9+36), np.sqrt(16+16)
print("Matrix's column vector, l2 norm, axis=0:\n",np.linalg.norm(x,axis=0,keepdims=True))

print("***********************")
# max(0+1, 3+6, 4+4)
print("Matrix's l1 norm, ord=1:",np.linalg.norm(x,ord=1,keepdims=True))
print("Matrix's l2 norm, ord=2:",np.linalg.norm(x,ord=2,keepdims=True))
# max(0+3+4, 1+6+4)
print("Matrix's ∞ norm, ord=np.inf:",np.linalg.norm(x,ord=np.inf,keepdims=True))

print("***********************")
print("Matrix's row vector, l1 norm, ord=1, axis=1:\n",np.linalg.norm(x,ord=1,axis=1,keepdims=True))
print("Matrix's row vector, l1 norm, ord=1, axis=1, keepdims=False:\n",np.linalg.norm(x,ord=1,axis=1,keepdims=False))

######### Output #########
"""
Default(sqrt of square sum of all elements, does not return matrix), keepdims=False:
 8.831760866327848
Sqrt of square sum of all elements, return matrix, keepdims=True:
 [[8.83176087]]
***********************
Matrix's row vector, l2 norm, axis=1:
 [[5.        ]
 [7.28010989]]
Matrix's column vector, l2 norm, axis=0:
 [[1.         6.70820393 5.65685425]]
***********************
Matrix's l1 norm, ord=1: [[9.]]
Matrix's l2 norm, ord=2: [[8.70457079]]
Matrix's ∞ norm, ord=np.inf: [[11.]]
***********************
Matrix's row vector, l1 norm, ord=1, axis=1:
 [[ 7.]
 [11.]]
Matrix's row vector, l1 norm, ord=1, axis=1, keepdims=False:
 [ 7. 11.]
"""
parameter description computation
ord=1 l1l_1 norm |x1x_1|+|x2x_2|+...+|xnx_n|
Default l2l_2 norm x12+x22+...+xn2\sqrt{x_1^2+x_2^2+...+x_n^2}
ord=∞ l∞l_∞ norm max( |xix_i| )

ord=1: Maximum of each column's sum
ord=∞: Maximum of each row's sum
ord=2: Find the eigenvalue, then find the maximum square of the eigenvalue.

ans = np.mat(x).T*np.mat(x)
[x,y] = np.linalg.eig(ans))
max(np.sqrt(x))

axis: process rule
axis=0: processing by column vectors and finds the norm of multiple column vectors
axis=1: processing by row vectors and finds the norm of multiple row vectors
axis=None: Matrix's norm

keepdims: whether to maintain the two-dimensional characteristics of the matrix