Decision Tree is one of classical algorithms in machine learning. It can be used as both a classification model and a regression model. It is also suitable as a ensemble model, such as Random Forest. The history of Desicion Tree has three stages: ID3, C4.5 and CART

[toc]

1. The Information Theory Foundation of Decision Tree ID3

It all originated from a simple "if...else..." statment that every programmer almost uses every day. Data researchers want to use a certain condition (if...else...) to split dataset into two distinct subsets. Then there are two questions we need to consider:

• A dataset usually has lots of features. So how to choose the feature that we need to use first in "if...else..."? And second, third features?
• How to quantitatively evaluate the quality of a certain binary division on the feature?

In 1970s, a genius Ross Quinlan invented a method to guide and evaluate the process of decision tree by using entropy in information theory. As soon as the methods came out, its simplicity and efficiency cause a sensation. Quinlan called it ID3 algorithm.

Entropy measures the uncertainty of things, the more uncertain things, the greater the entropy of it. Specifically, the expression of the entropy of a random discrete variable X is as follows:

$H(X) = - \sum_{i=1}^np_ilog(p_i)$

n represents the "n" kinds of discrete values. (counts of unique value of X)
$p_i$ is the probability that X takes the value "i".
log usually is the logarithm based on 2 or e.

For example, if X only has two kind of values, the entropy is the largest when the probabilities of this two values are 1/2, which means X has the largest uncertainty. H(X) = -(1/2*log(1/2) + 1/2*log(1/2)) = log(2)
if the probabilities of this two values are 1/3 and 2/3, H(X) = -(1/3*log(1/3) + 2/3*log(2/3)) = log(3) - 2/3*log(2) < log(2)

Then multivariable entropy:

$H(X,Y) = - \sum_{i=1}^n p(x_i,y_i)log(p(x_i,y_i))$

And conditional entropy H(X|Y), which is the uncertainty of X after knowing the uncertainty of Y:

$\begin{aligned} H(X|Y) &= - \sum_{i=1}^n p(x_i,y_i)log(p(x_i|y_i)) \\ &= \sum_{j=1}^n p(y_j)H(X|y_j) \end{aligned}$

H(X) represents the uncertainty of X.
H(X|Y) represents the left uncertainty of X after knowing the Y.
Therfore, [H(X) - H(X|Y)] represents the degree of reduction in uncertainty of X after knowing the Y. It is also called mutual information in information theory, which is wrote as I(X,Y). (互信息)
In decision tree ID3 algorithm, mutual info is called information gain (信息增益).

ID3 algorithm uses information gain to determin what feature should be used in current node to build the decidion tree. The larger the information gain, the better it is for classification in current node.

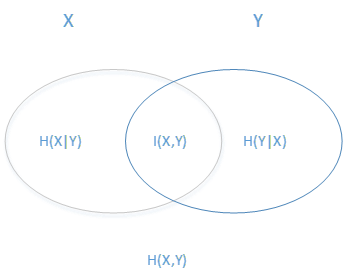
From the graph above, we can easily figure out the relationship among them.

The ellipse on the left represents H(X) [uncertainty of X]. And the ellipse on the left represents H(Y).
The overlapping section in the middle is the mutual information (or information gain) I(x,y).
The left section of left ellipse H(X|Y)
The union of two ellipse is H(X,Y)

If Y is "a", almost all X is "b". This means when Y is "a", the uncertainty of X is very low (H(X|Y) is very small, I(X,Y) is large). Because the randomness of the X value is very small when Y is "a". Then X is suitabale as a feature of classification of Y.

2. Decision Tree ID3 Algorithm Principle

Take an example for ID3 algorithm to see how it uses information gain to build a decision tree model.

Suppose there are 15 samples data D, the output is 0 or 1, and 9 of them are 1, 6 of them are 0.
There is a feature A in the sample, the values are A1, A2 or A3.
When A is A1, the output has 3 "1" and 2 "0"
When A is A2, the output has 2 "1" and 3 "0"
When A is A3, the output has 4 "1" and 1 "0"

The entropy of sample D is:

$H(D) = - (\frac{9}{15}log_2\frac{9}{15} + \frac{6}{15}log_2\frac{6}{15}) = 0.971$

The conditional entropy of sample D in the feature A is:

$\begin{aligned} H(D|A) &= \frac{5}{15}H(D_{A1}) + \frac{5}{15}H(D_{A2}) + \frac{5}{15}H(D_{A3}) \\ &= -\frac{5}{15}(\frac{3}{5}log_2\frac{3}{5}+\frac{2}{5}log_2\frac{2}{5}) -\frac{5}{15}(\frac{2}{5}log_2\frac{2}{5}+\frac{3}{5}log_2\frac{3}{5}) -\frac{5}{15}(\frac{4}{5}log_2\frac{4}{5}+\frac{1}{5}log_2\frac{1}{5}) \\ &= 0.888 \end{aligned}$

Then the information gain H(D) - H(D|A) = 0.971 - 0.888 = 0.083

The specific algorithm process looks like:

Input is "m” samples, the sample output set is "D".
Each sample has "n" discrete features, the feature set is "A".
The final output of ID3 algorithm is a decision tree "T"

The process is:

1. Initialize the threshold of information gain $\epsilon$
2. Read the output set D. If all output value are same "Di", return a single node tree T, marked as category "Di".
3. Read the feature set A. If A is null, return a single node tree T, marked as the category that has the largest counts number in D. [argmax(counts(Di))]
4. Traverse and Calculate the information gain of each feature in A (n features). Select the feature "$A_g$" which has the largest information gain.
5. If the information gain of "$A_g$" is less than the threshold $\epsilon$, return a single node tree T, marked as the category that has the largest counts number in D. [argmax(counts(Di))]
6. If not (else), according to the different values in $A_g$, split the total sample into several different categories subset $D_j$. Each category is a child node. And return the tree T with multiple nodes.
7. For each child nodes, let $D=D_j, A=A-\{A_g\}$, then recursively call the step 2-6 to get and return the subtree $T_i$.

3. Deficiency of decision tree ID3 algorithm

Althogh ID3 algorithm proposed new ideas, there are still many areas worthy of improvement.

  (1) ID3 doesn't consider continuous features, such as length, density or other continuous features. This greatly limits the use of ID3.

  (2) ID3 uses the features of large information gain to preferentially establish the nodes of the decision tree. However, under the same conditions, the feature with more kinds of values has larger information gain. For example, if the feature A has 2 kinds of values, each of them is 1/2, H(A)=log(2); if the feature A has 3 kinds of values, each of them is 1/3, H(A)=log(3). How to correct this problem?

  (3) ID3 doesn't consider the condition of missing values.

  (4) ID3 doesn't consider the overfitting problem.

Ross Quinlan has improved the ID3 algorithm based on the above deficiencies. This is C4.5 algorithm.

The reason that why the new algorithm wasn't named ID4 or IDn:
Decision tree was too popular when it came out, then lots of people started the second innovation and occupied ID4 and ID5 soon. So Quinlan took a new path and named it the C4.0 algorithm. And later, the advanced version was C4.5 algorithm.

---

4. Improvement of the Decision Tree C4.5 algorithm

According to the 4 deficiencies of ID3 above, C4.5 improved them through the following:

(1) Cannot handle continuous features:

The idea of C4.5 is to discretize continuous features. For example, the feature A of m samples has m values, sort from small to large as $a_1, a_2, ..., a_m$. C4.5 take the average value between two neighbor values as a dividing point, then there are (m-1) dividing points. The i-th dividing point $T_i$ is $T_i=\frac{a_i+a_{i+1}}{2}$.

For these (m-1) dividing points, C4.5 calculates the information gain using each dividding point as the binary classification point. Finally, select the point with the largest information gain as the binary discrete classification point for the continuous feature.

Pay attention: unlike the discrete attribute, if the current node is a continuous attribute, then this attribute can also participate in the generation and selection process of child nodes.

(2) Bias of features with more kinds of values:

C4.5 inroduces a new variable of information gain ratio $I_R(X,Y)$. It is the ratio of information gain and feature entropy.

$I_R(D,A) = \frac{I(A,D)}{H_A(D)}$

D is the output set of samples, A is the feature set. And the feature entropy is:

$H_A(D) = -\sum_{i=1}^n\frac{|D_i|}{|D|}log_2\frac{|D_i|}{|D|}$

n is the number of categories of feature A.
$D_i$ is the number of samples corresponding to the i-th value of feature A.
D is the total number of all samples.

The feature with more kinds of values has a larger feature entropy. It serves as a denominator to correct the problem that information gain tends to be biased toward features with more values.

(3) Problem of missing values:

There are two sub problems needed to be solved:

a. How to choose the feature to build chind node when some features of the sample is missing?
b. If the feature is selected, how to deal with the samples with missing values on this feature?

• a. Feature Choosing with missing value

  For a featur A with missing values, C4.5 set a weight for each sample (including those with missing value in A), the initial weight could be 1. Then C4.5 splits the data into 2 subsets, one is the data D1 without missing value, the other one is the data D2 with missing value.

For no missing value data D1, calculate the information gain ratio with weight, and then multiply by a coefficient, which is the ratio of weighted samples with no feature A missing and weighted total samples.

• b. Data Spliting with missing value in A

  C4.5 can divide the samples with missing value A into all child nodes at the same time. But the weight of this sample is reassigned according to the proportion of the number of samples of each child node.

For example, suppose there is a sample "ms" with missing value in feature A. The feature A has 3 kinds of value: A1, A2 and A3, and the number of samples are respectively 2,3,4, that is, the proportion of A1, A2 and A3 are 2/9, 3/9 and 4/9. Then the corresponding weights of missing value sample are adjusted to 2/9, 3/9 and 4/9.

(4) Overfitting problem:

C4.5 introduced regularization coefficients for preliminary pruning, which will be discussed in detail later.

5. Deficiency of decision tree C4.5 algorithm

Althogh C4.5 algorithm improves ID3 a lot, there are still some areas worthy of improvement.

  (1) ID3 and C4.5 algorithms generate a multi-fork tree. Discrete feature with more than 2 kinds of value leads multiple child nodes. In many cases, the binary tree model in the computer will be more efficient than the multi-tree operation. Binary tree can improve efficiency.

  (2) C4.5 can only be used for classification. If the decision tree can be also used for regression, its scope of use can be expanded.

  (3) C4.5 uses the entropy model, there are lots of time-consuming logarithmic operations. If it is continuous feature, there is also a time-consuming sorting operation. It would be better if the model simplification can reduce the computational intensity without sacrificing too much accuracy.

  (4) Decision tree algorithm is very easy to overfit, the generated decision tree must be pruned. C4.5's pruning method still has room for optimization. There are two main ideas for pruning:

• pre-pruning, which is to decide whether to pruning when a decision tree is generated.
• post-pruning, that is, the decision tree is generated first, and then pruned tree through cross-validation.

In the next section when we talk about the CART tree, we will specifically introduce the idea of reducing the branch of the decision tree, which mainly uses post-pruning plus cross-validation to select the most suitable decision tree.

These 4 problems has been improved in CART algorithm. So if not consider integrated learning at present, in the ordinary decision tree algorithm, the CART algorithm is considered to be the better algorithm.

---

6. CART Classification Tree Algorithm -- Gini Coefficient

Let's review at first, as we all know now:

• ID3 uses information gain to select features. $I(D,A) = H(D)-H(D|A)$
• C4.5 uses information gain ratio to select features. $I_R(D,A)=\frac{I(A.D)}{H_A(D)}$

Both of them are entropy models based on the information theory, $H(X) = -\sum_{i=1}^n p_i*log(p_i)$, which has lots of logarithmic computation and decrease the efficiency a lot. Is there any method we can simplify the model to increase the efficiency but without sacrificing too much accuracy? Yes, It is Gini Coefficient of CART. The Gini Coefficient represents the impureness of the node. The smaller the Gini, the lower the unpurification, the better classfication. This is opposite to Information Gain (Ratio)

Specifically, in a classification problem, supposed there are K categories, and the probability of i-th category is $p_i$. Then the Gini coefficient is:

$Gini(p) = \sum_{i=1}^K p_i(1-p_i) = 1-\sum_{i=1}^Kp_i^2$

If there is a binary classification, and the probability of first category is p, the Gini Coefficient is super easy: $Gini(p) = 2p(1-p)$

For a sample D, if it has K categories, and the counts of i-th category is $|C_i|$, and the total number of D is |D|, then the Gini Coefficient of sample D is:

$Gini(D) = 1 - \sum_{i=1}^K \left(\frac{|C_i|}{|D|}\right)^2$

And if the feature A (binary discrete or continuous) split the data into two subsets D1 and D2 by a certain value a of A. Then in the condition of feature A, the Gini Coefficient of D is:

$Gini(D,A) = \frac{|D_1|}{|D|}Gini(D_1) + \frac{|D_2|}{|D|}Gini(D_2)$

Comparing with entropy model formulas, the Quadratic computation of Gini Coefficient is easier a lot than logrithmic computation, especially in the binary classification. And so, Compared with the entropy model, how does the Gini coefficient perform? Take a look at the plot below.

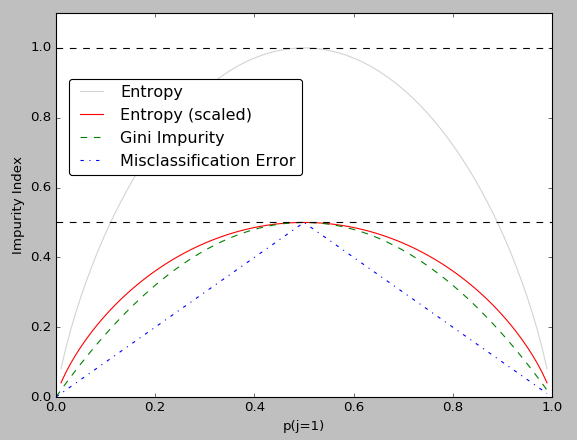
As we can see from the plot, the curves of Gini and Entropy (scaled) are very close, and the error is only slightly larger near the angle of 45 degrees. Therefore, the Gini can be used as an approximate substitute for the entropy model. In fact, the CART use Gini to select features of decision tree. And for further simplification, CART only divides each node to binary child nodes but not multi-nodes, so that the CART classification tree algorithm builds a binary tree instead of a multi-tree. In this way, the calculation of the Gini coefficient can be further simplified, and a more elegant binary tree model can be established.

7. CART Algorithm on continuous features and discrete features

continuous features

The idea of CART on continuous features is same with C4.5.
Suppose the sample m has m values in continous feature A, CART sorts them from small to large, $a_1,a_2,...,a_m$ and finds out (m-1) dividing points, which is the average value of each pair of neighbor points. For example, the i-th dividing point $T_i$ is $\frac{a_i+a_{i+1}}{2}$. CART calculates the Gini Coefficient value of each one of the dividing points, and selects the point with the lowest Gini Coefficient value.

Pay attention: Unlike ID3, if the current node is the continuous feature, it will be still used in the following steps to create other child nodes.

discrete features

Unlike ID3 and C4.5, CART uses a non-stop binary classification, no matter how many kinds of values the feature has. For example, if the feature A has A1, A2, A3 three kinds of values, ID3 or C4.5 will build three child nodes {A1},{A2} and {A3}. But CART will consider 3 binary child nodes conditions: {A1} and {A2,A3}, {A2} and {A1,A3}, {A3} and {A1,A2}, then select the condition with lowest Gini Coefficient. And if CART selects {A2} and {A1,A3}, due to the value of feature A is not completely separated this time, CART will have the opportunity to continue to select feature A to divide A1 and A3 in the child node.

Pay attention: In ID3 or C4.5, discrete feature will only participate in the establishment of a node once, because they builds multi-division tree. Unlike them, CART will reuse each discrete feature.

Regardless of continuous features or discrete features, after the current node uses this feature to build a subtree, CART will still use this feature in the future subtree establishment.

8. CART classification tree establishment algorithm specific process

The input of CART algorithm are training set D, threshold of Gini Coefficient, threshold of number of samples
The outpuf of CART is the decision tree T

CART algorithm starts from the root node, and uses the training set to recursively build the CART tree:

1. For the dataset D of current node, if the number of records is smaller than the threshold number of samples, or there are no features, then return the decision subtree T, and current node stops recursive.

2. Calculate the Gini Coefficient of dataset D of current node, $Gini(D)$. If the Gini Coefficient is smaller than the threshold, then return the decision subtree T, and current node stops recursive.

3. Calculate the Gini Coefficient of each feature value of the current node on the data set D, $Gini(D,A)$. The processing of missing values is the same as that described in the C4.5 algorithm.

4. Among all calculated Gini Coefficients of the pair of each feature and each feature's possible dividing point, choose the feature with the appropriate dividing point value that has smallest Gini Coefficient. According to this optimal feature and optimal feature value (dividing point), the dataset of current node is divided into two nodes D1 and D2, and the left and right nodes of the current node are established at the same time, the dataset D of the left node is D1, and the dataset D of the right node is D2.

5. Steps 1-4 are recursively called on each of the left and right child nodes to generate a decision tree.

When doing the prediction on the generated decision tree, if the sample "P" in prediction set falls into a certain leaf node, and there are multiple training samples in each leaf node, then the category prediction of sample "P" is the category with the highest probability in this leaf node.

9. CART regression tree building algorithm

One advantage of CART is that it can be used not only as a classification model but also as a regression model.

If the output of sample is the discrete value, we should train a classification tree. However, if the output of sample is the continuous value, we should train a regression tree.

The algorithms for building CART regression trees and CART classification trees are mostly similar, so here we only discuss the differences between the algorithms for building CART regression trees and CART classification trees.

The main difference between the establishment and prediction of CART regression tree and CART classification tree:

• Different methods for processing features.
• Different ways of making predictions after the decision tree is established.

In feature selection and division, CART classification tree uses the Gini Coefficient to measure the pros and cons of each division node, which is suitable for classification problem. However, for the regression problem, we use variance measurement methods. The goal of the CART regression tree is that:

• For the data sets D1 and D2 divided on both sides of the arbitrary division feature "A" and the division point "s"
• Find the feature and feature division point corresponding to the minimum mean square deviation of each set of D1 and D2, and the minimum sum of mean square errors of D1 and D2.

$\min_{A,s}\left[\min_{c_1} \sum_{x_i \in D_1(A,s)}(y_i-c_1)^2 + \min_{c_2} \sum_{x_i \in D_2(A,s)}(y_i-c_2)^2 \right]$

(A,s) is the optimal feature and optimal division point of optimal feature. This is what we need in building decision tree.
$c_1$ and $c_2$ are the average output value of dataset D1 and D2.
(A,s) should minimize the above formula (Loss Function)

In the prediction after the decision tree is established, the output of the regression tree is not a category. It uses the mean or median of the output value in final leaves to predict the output.

Except for the above, there is no difference between CART regression tree and CART classification tree building algorithm and prediction.

10. Pruning of CART tree algorithm

Since the decision tree algo is easy to overfitting after training, resulting in poor generalization ability. In order to preventing the overfitting problem, we need to prune the CART tree, that is, similar to regularization of the linear regression to increase the generalization ability.

The pruning algorithm of the CART tree can be summarized in two steps:

• Generate various pruned decision tree from the original decision tree.
• Use cross-validation to test the prediction ability for all pruned tree. And the tree with the best generalization prediction ability is selected as the final CART tree.

a. loss function of decision tree

The pruning strategies of the CART regression tree and the CART classification tree are that one uses the mean square error and one uses the Gini coefficient when measuring the loss.

There is a Classification tree T, |T| is the number of leaf nodes in the tree. "t" is one of leaf node of tree T:

• $N_t$ is the number of samples in leaf node "t", $H_t(T)$ is the entropy of leaf node "t".
• In leaf node "t", the number of k-th category samples is $N_{tk}$, k=1,2,...,K. (There are K categories in the nod)
• $\alpha \ge 0$ is the regularization coefficient

Then the loss function of this classification decision tree $C_{\alpha}(T)$ is:

$C_{\alpha}(T) = \sum_{t=1}^{|T|}N_tH_t(T) + \alpha|T|$

The entropy of node "t", $H_t(T)$ is:

$H_t(T) = - \sum_{k=1}^K \frac{N_{tk}}{N_t} log(\frac{N_{tk}}{N_t})$

We defined C(T) as the prediction error of the model on the training data, which can also represents the degree of fitting between the model and the training data.

$\begin{aligned} C(T) &= \sum_{t=1}^{|T|}N_tH_t(T) \\ &= - \sum_{t=1}^{|T|} \sum_{k=1}^K N_{tk}*log(\frac{N_{tk}}{N_t}) \end{aligned}$

Then the loss function $C_{\alpha}(T)$ can be written as:

$C_{\alpha}(T) = C(T) + \alpha|T|$

Whether it is Classification Tree (CT) or Regression Tree (RT), their loss function formula is same: $ C_{\alpha}(T) = C(T) + \alpha|T| $. The only difference is the calculation of prediction error C(T), which uses entroy or Gini coefficient in CT, and mean squared error in RT.

Emphasize again, the loss function of decision tree:

$C_{\alpha}(T) = C(T) + \alpha|T|$

C(T) is the prediction error of the decision tree, or the degree of fitting between training data and the tree model.
|T| is the number of leaf nodes in the tree, which can represent the complexity of the tree model.

So we can easily find that, C(T) and |T| are two controdictory values.

A very small C(T) means that the degree of fitting between the model and the training data is very high, and the prediction result of the training set is very accurate (but the performance of test data is hard to say). Then complexity |T| should be very large.

Similarly, a simple tree with low |T| (low complexity) has large C(T) (high prediction error in training set).

The goal is to balance the accuracy and complexity of the model so that the combined loss function of the two is minimal.

$\alpha \ge 0$ is also an important coefficient in the loss function.

• $\alpha$ is large => prompt to choose a simpler tree (small |T|)
• $\alpha$ is small => prompt to choose a more complex tree (large |T|)
• $\alpha$ is 0 => No pruning, current tree is the optimal. Only consider the fitting between model and data, and ignore the model complexity. (easily cause overfitting)
• $\alpha$ is $+\infty$ => All pruning, only the root node is left.

So pruning means when $\alpha$ is determined, select a Tree model with the least loss function value $C_{\alpha}(T)$.
General speaking, the larger the $\alpha$ is, the stronger the pruning is, and the smaller the optimal tree is (compared with the original decision tree)
For a fixed $\alpha$, there must be a unique subtree that minimizes the loss function $C_{\alpha}(T)$.

b. idea of pruning

All above is the method of measuring the loss function of pruning tree. And the next is the idea of pruning.

For any subtree $T_t$ at the node t, if no pruning, its original loss is:

$C_{\alpha}(T_t) = C(T_t) + \alpha|T_t|$

$|T_t|$ is the total number of leaf nodes of the node "t".

If prune the node "t" and only the root node is left, its loss after pruning is:

$C_{\alpha}(t) = C(t) + \alpha$

Since, only the root node as one leaf node is left after pruning. $\alpha|t| = \alpha$

Subtree "$T_t$" is more complex than subtree "t", the error $C(T_t) \le C(t)$. So, if $\alpha$ is 0 or very small, $C_{\alpha}(T_t) \le C_{\alpha}(t)$. When $\alpha$ increases to a certain degree, it will meet:

$C_{\alpha}(T_t) = C_{\alpha}(t)$

If $\alpha$ continues to increase, then $C_{\alpha}(T_t) \ge C_{\alpha}(t)$. In other words, the critical value of $\alpha$ derived from the equality before and after pruning is:

$\begin{aligned} C(T_t) + \alpha|T| &= C(t) + \alpha \\ \alpha &= \frac{C(t)-C(T_t)}{|T|-1} \end{aligned}$

In the pruning of node "t"
Before pruning, lost of "t": $C_{\alpha}(T_t)$
After pruning, lost of "t": $C_{\alpha}(t)$
There are 3 conditions of loss value after pruning: increase, unchange or decrease.
If the loss value doesn't increase after pruning, that is, if $C_{\alpha}(T_t) \ge C_{\alpha}(t)$, then pruning the subtree is better. It shows that complexity plays a key role, and the loss function plays a small role. In simple terms, the leaf nodes before pruning do not improve the accuracy but bring more complicated trees.

c. CART pruning algorithm process

Since, for a fixed $\alpha$, there must be a unique subtree that minimizes the loss function $C_{\alpha}(T)$. We can mark this subtree as $T_{\alpha}$

Breiman has proved that the tree can be pruned recursively. Increase $\alpha$ from small to large, $a_0 < a_1 < ... < a_n < +\infty$, producing a series of intervals $[a_i,a_{i+1})$, i=0,1,2,...,n. The optimal subtree sequence obtained by pruning is {$T_0,T_1,...,T_n$}

Then in the optimal subtree sequence {$T_0,T_1,...,T_n$}, select the optimal subtree $T_{\alpha}$ through cross-validation.

The CART pruning algorithm:
Input: the original decision tree $T_0$ obtained by the CART tree algorithm in section 8.
Output: Optimal decision subtree $T_{\alpha}$
The algorithm process:

1. Initialize $\alpha_{min}=+\infty$, Set of optimal subtree $w = \{T_0\}$
2. Calculate $C_{\alpha}(T_t), |T_t|, \alpha$
   • Calculate the training error loss function $C_{\alpha}(T_t)$ of each internal node "t" from the leaf node from bottom to top. (The regression tree is the mean square error, and the classification tree is the Gini coefficient).
   • Calculate the total number of leaf nodes of "t", $|T_t|$, and
   • Calculate the threshold of regularization cofficient $\alpha= \min \left\{\frac{C(t)-C(T_t)}{|T_t|-1}, \alpha_{min} \right\}$
   • Update the $\alpha_{min} = \alpha$
3. Get the set M of $\alpha$ values for all nodes.
4. Chosse the smallest regularization coefficient value $\alpha_k$ from the set M, then access the internal nodes "t" from top to bottom. If $\frac{C(t)-C(T_t)}{|T_t|-1} \le \alpha_{k}$, pruning is performed.
   • And determine the value of the leaf node t. If it is a classification tree, it is the category with the highest probability; if it is a regression tree, it is the average of all sample outputs.
   • The optimal subtree corresponding to the regularization coefficient $\alpha_{k}$ is obtained $T_k$
5. Update the optimal subtree set $w = w \cup T_k$, and regularization coefficient set $M=M-\{\alpha_k\}$
6. If $w$ is not null, back to step 4. Else, all optimal subtrees with different $\alpha$ have been obtained in set $w$.
7. Use cross-validation to test the prediction accuracy for all pruned tree in optimal subtree set $w$. And the tree with the best generalization prediction ability is returned as the final CART tree.

11. Summary of CART algorithm

Algorithms	Model Support	Tree Structure	Feature Selection	Continuous Feature	Missing Value	Pruning
ID3	Classification	General Tree (Multitree)	Information Gain	Not Support	Not Support	Not Support
C4.5	Classification	General Tree (Multitree)	Information Gain Ratio	Support	Support	Support
CART	Classification & Regression	Binary Tree	Gini Coefficient; Mean Square Error	Support	Support	Support

The CART algorithm still has some shortcomings:

1. Whether it is ID3, C4.5 or CART, when making feature selection, they all choose the best one feature to build the decision tree node. However, in some case, the classification decision should not be determined by only one certain feature, but should be determined by a set of features. The decision tree obtained in this way is more accurate, which is called a multi-variate decision tree. When selecting the optimal feature, the multivariate decision tree does not select one certain optimal feature, but selects an optimal linear combination of features to make a decision. The representative of multi-variate decision tree algorithm is "OC1".
2. If the sample changes a little bit, it will cause a dramatic change in the tree structure. This can be solved by ensemble models, such as random forest in integrated learning.

12. Summary of Decision Tree

Advantages of Decision Tree:

1. The generated decision tree is very simple and intuitive.
2. Basically no preprocessing is needed, such as normalization in advance, and missing values preprocessing.
3. The cost in prediction of decision tree is $O(log_2m)$, m is the number of samples.
4. Both discrete and continuous values can be processed. Many algorithms only focus on discrete values or continuous values.
5. It can deal with multi categories classification problem.
6. Compared with the black box classification model such as neural network, the decision tree can be well explained logically.
7. Cross-validated pruning can be used to filter the model, thereby improving the generalization ability.
8. High tolerance for some abnormal points.

Disadvantages of Decision Tree:

1. Decision tree algorithm is very easy to overfit, resulting in weak generalization ability. It can be improved by setting the minimum sample number of nodes and limiting the depth of decision tree.
2. The decision tree structure will change dramatically when sample changes a little bit. This can be solved by ensemble models such as random forest.
3. Finding the optimal decision tree is an NP-hard problem. We usually get into the local optimal by heuristic method. It can be improved by methods such as integrated learning.
4. For some more complex relationships, decision trees are difficult to learn, such as XOR. There is no way for this. Generally, this relationship can be solved by using neural network classification methods.
5. If the sample ratio of certain features is too large, generating decision trees tends to favor these features. This can be improved by adjusting the sample weights.